Although a MIT mathematician confirmed Tamar Barbi’s discovery of a working theorem she used solving geometry homework problems wasn’t previously known, she still prefers a future in theater rather than mathematics.

By Yael Branovsky

Tamar Barbi from Hod Hasharon is only in the 10th grade, but she has already chalked up an impressive achievement: developing a new geometric theorem.

Israeli 10th grader, Tamar Barbi: The theorem is very logical and basic.

Barbi, who is studying mathematics on the highest matriculation track offered in Israel, discovered while doing her geometry homework that the theorem she was using to solve one of the problems on her homework didn’t actually exist.

“I checked with my teacher, Sean Gabriel-Morris, I asked relatives abroad who are involved with mathematics, and I consulted my parents, and [then] I realized that the theorem really didn’t appear anywhere, even though it’s very logical and basic.”

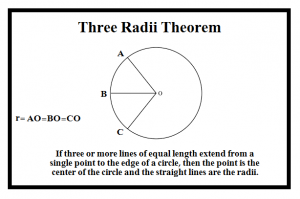
According to the new “Three Radii Theorem,” if three or more equal lines extend from a single point to the edge of a circle, then the point is the center of the circle and the straight lines are the radii.

Gabriel-Morris, a former chef who retrained as a math teacher, worked with Tamar to research the subject and helped her develop the new mathematical theorem, proving that it could serve as an easy, convenient solution for many geometry problems. The teacher-student team sent the theorem along with proof to a mathematician from the Massachusetts Institute of Technology, who became excited and wrote back that “it’s good to see how Tamar’s theorem provides elegant proof for other important mathematical theorems.”

The proof was also sent to math lecturers at the University of Haifa, and Barbi and Gabriel-Morris were invited to give a lecture on it to some of the top math instructors in Israel.

Barbi remains unexcited. She is involved with theater arts, studies acting, plays the piano and the guitar, sings, and dances.

“I don’t think math will become my profession. I hope to work in theater arts,” Barbi says.

Eli Hurvitz, executive director of the Trump Foundation, which promotes math and science studies in Israel, said: “Once again, it’s been proven that a great teacher, who challenges and supports [students], along with an ambitious and curious student, are a winning combination.”

Hurvitz added that in the future, Israeli students would use math to “develop medicines and technologies and make scientific breakthroughs.”

View original Israel Hayom publication at:
http://www.israelhayom.com/site/newsletter_article.php?id=32345

Liked this post? well,
One click, and you can download our free App